第42回 四方山話(24) 論理思考のススメ1
こんにちは、キャリア・コンサルタント高橋です。
これまで5回に渡り、水平思考の考え方をご紹介してきました。水平思考は自由な発想で物事の本質をとらえる思考法ですので、何かを創造したりイノベーションを起こすことには適しているといえます。しかし、普段の仕事や生活を考えると、物事を論理的に考える、論理だてて会話ができるといった論理的な思考がよく使われます。そこで、「○○のススメ」シリーズの第2段として、今度は論理思考ネタを取りあげてみたいと思います。
■問題を解決できない人
水平思考のコラムでもお話しましたが、思考法や考え方は何かしらの問題を解決するためにあります。例えば、
- 現場の先輩から言われた課題が期日までにできない
- 今、起きているトラブルの解決方法が分からない
- 仕事の進ちょくがはかどらず、どのようにしたらよいか分からない
こういった問題は仕事だけに留まらず、普段の日常生活にもあふれ返っています。そして、その解決方法は人によってさまざまです。
- 分からないことは人に聞く
- 徹底的に調べてみる
- 後回しにして、まずはできることから手を付ける
しかし、こういった答えを出せない人もおられます。それは、その人の資質に問題があることもありますが、筆者の経験からすれば、その人に問題を解決する能力がないということではなく、単に問題を解決する方法を知らないことの方が圧倒的に多いです。
でも、それはよく考えれば当たり前の話です。義務教育は小学校6年間+中学校3年間の計9年間ありますが、その間、問題解決の授業なんて1度もありません。大学やビジネススクールまで行けばそのようなそのような講義や授業を受ける機会もあるでしょうが、大半の人はそういった講義や授業の存在すら知りません。そのように考えたら、問題を解決する方法を知らなくても何らおかしいことではないと思います。
そこで、今回から数回に渡り、論理思考(ロジカル・シンキング)という思考法を使って問題を解決する方法を考えてみたいと思います。これまで物事を論理的に考えることができなかった、問題点の解決方法を自分ひとりで見つけることができなかった、物事をうまく相手に説明することができなかった……、このような悩みを持っている人にとっては、論理思考の考え方が役に立つかもしれません。ぜひ、使ってみてください!
■論理思考に必要な2つの要素
論理思考と一口にいってもその範囲は非常に広いです。なぞかけ※のようなモノから、プロジェクト・マネジメントで使われるデシジョン・ツリー分析※などもすべて論理思考です。そのため、ここでは論理思考を学ぶ上で必要な要素を考え、そこから論理思考の考え方を掘り下げてみたいと思います。
※なぞかけ:「○○とかけまして、○○と解きます。その心は○○」のアレです。例えば、「キャリアとかけまして、登山と解きます。その心は、どちらものぼって(上って、登って)いこうとします」……、失礼しました。
※デシジョン・ツリー分析:「決定木」や「意思決定ツリー」と呼ばれ、意思決定の構造(しくみ)を樹形図のような形で表したモノ。詳しくはこちらもご参照ください。
《論理思考に必要な2つの要素》
- 論理的な考え方を身に付けること
- 問題解決のフローを身に付けること
論理思考を使って問題解決をする場合、問題を解決するためのフロー(流れ)にのっとり、順を追って問題を考えていきます。しかし、その過程では論理的な考え方が必要になるため、このコラムでは最初に論理的な考え方をご紹介した上で、問題解決のフローを使って実際の問題を考えてみようと思います。
■論理的な考え方を身に付ける
論理思考で物事を考える場合、物事を論理的に考えられるかが大きなポイントになります。「物事を論理的に考える」とは、大きく分けて以下の考え方で物事をとらえられているか? といい換えることができます。
- 「話の筋道が通っているか? 」
- 「選択肢の漏れがないか? 」
- 「論点がズレていないか? 」
これら3つの考え方はそれぞれがバラバラで独立しているモノではなく、それぞれに関連性があり、正しい関係性を保つことで論理的な考え方を成り立たせると考えます。これらの関連を図で表すと以下のようになります。
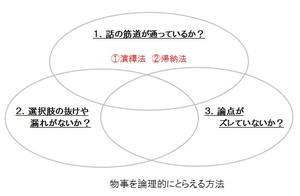
■「話の筋道が通っているか? 」
「話の筋道が通っているか? 」とは、話の筋道や理屈が通っているかを考えることです。例えば、プログラミングの進捗が遅れていた時の原因を論理的に考えてみます。この原因が、
「体調が悪かった」
「技術的な問題に直面した」
などの理由なら、一見すると話の筋道や理屈が通っているように考えられます※。しかし、その理由が、
「円高だったから」
「総理大臣が変わったから」
などの理由だとしたら、直接の関連性を見出すことができず、話の筋道や理屈が通っているようには考えられません。
※筋道や理屈が通っているように考えられます:実際には解答の妥当性(裏付け)を検証する必要がありますが、ここでは割愛します。
このように、物事を論理的に考えるためには、論理的に話が展開されているか(=話の筋道や理屈が通っているか)を意識する必要があります。そのための方法として、演繹(えんえき)法、帰納法という考え方があります。
■演繹(えんえき)法とは
演繹(えんえき)法というと聞き慣れない言葉ですが、「三段論法※」といえばご存知の方もいるのではないでしょうか。この考え方は、2つの情報を関連付けて、そこから結論を導き出す方法※です。例えば、以下の例をみてください。
――
情報1:人間はいつか死ぬ
情報2:ソクラテスは人間だ
↓
結論 :ソクラテスはいつか死ぬ
――
これは演繹法では非常に有名な命題です。情報1と情報2を関連付けたモノが結論になっています。もう一つみてみましょう。
――
情報1:このプログラミングにはJavaの技術力が必要だ
情報2:田中さんにはJavaのスキルがない
↓
結論 :田中さんはこのプログラミングができない
――
これも先ほどの例と同様、情報1と情報2を関連付けたモノが結論になっています。このように演繹法では、ある結論を導き出すために2つの情報を結び付けています。このとき、結論は2つの情報を矛盾がないように結びつけなければなりません。
※三段論法:実際の三段論法はもう少し深い考え方がありますが、ここでは概要レベルを理解する程度でOKです。詳しく知りたい方はこちらをご参照ください。
■それでは問題です!
それでは、実際に演繹法を使って問題を解いてみましょう。意識することは「結論は2つの情報を矛盾がないように結びつける! 」です。
――
《問題》
情報1:喫煙者は禁煙者より肺ガンの発生確率が高い
情報2:加藤さんは喫煙者、木下さんは禁煙者だ
↓
結論 :???
――
問題が簡単で拍子抜けされましたか? 答えは、このようになりますね。
結論 :木下さんより加藤さんの方が喫煙による肺ガンの発生確率が高い
ちゃんと結論の内容と情報1と情報2は矛盾なく結び付いています。もし、うまく答えが出せなかった場合、結論の前に「だから~」を付け加えて考えてみてください。そうすると、ストーリーができて、考えがまとまりやすくなります。
■帰納法とは
帰納法というと数学的帰納法※という言葉がありますが、ここでは、いくつかの情報から全てに共通する事柄を選び出す方法と考えてください。以下の例をみてください。
――
情報1:ソクラテスはいつか死ぬ
情報2:アリストテレスはいつか死ぬ
情報3:プラトンはいつか死ぬ
↓
結論 :人はいつか死ぬ
――
先ほどの演繹法とは逆に、それぞれの情報から全てに共通する事柄(ここでは人)を選び出しています。帰納法でも演繹法と同様に、情報と結論は矛盾なく結び付かなければなりません。それでは、もう一つの例をみてください。
――
情報1:ネズミaはネコをみたら逃げ出した
情報2:ネズミbはネコをみたら逃げ出した
情報3:ネズミcはネコをみたら逃げ出した
↓
結論 :ネズミはネコをみたら逃げ出す
――
これはどうでしょうか? この3つの情報だけをみると情報と結論は矛盾なく結び付いているようにみえます。しかし、ひょっとしたらネズミdはネコをみても逃げ出さないかもしれません。そうなるとこの例は正しくないかもしれません。このように、帰納法では範囲※によっては結論が変わる場合があります。そのため、帰納法を考える場合は一般的な範囲にもとづいて考える※ことが推奨されます。
※数学的帰納法:自然数に関する命題P(n)が全てのnに対して成り立っている事を証明するための方法。詳しく知りたい方はこちらをご参照ください。ちなみに、数学的帰納法はなぜか演繹法の考え方になっているそうです。
※情報の範囲:範囲をネズミa~ネズミcに限定すれば、この例は正しくなります。
※一般的な範囲にもとづいて考える:このような考え方を一般化といいます。ただし、一般化を考えると難しくなる場合がありますので、ここではできる範囲で考える程度でOKです。
■再び、問題です!
それでは、帰納法の問題も1つ出してみます。範囲も意識しながら考えてみてください。
――
《問題》
情報1:詳細設計書が納期までにでき上がっていない
情報2:経験不足のプロジェクトメンバーが多数増員された
情報3:仕様変更が頻繁に発生する
↓
結論 :???
――
何となくデスマーチっぽい状況ですが、ここからどのような結論が導きだせるでしょうか。これはいろいろな答えが考えられそうです。筆者はこのように考えてみました。
結論 :このプロジェクトの工数が肥大する可能性がある、このプロジェクトのリスクが高まっている、このプロジェクトのコストが上がっている、など
帰納法の場合、とらえ方によってはいくつかの答えが出てくる場合があります。しかし、どのような答えであっても、範囲を意識※して、情報と結論は矛盾なく結び付いていなければなりません。もし、帰納法でうまく答えが出せなかった場合、結論の前に「これらをまとめると~」を付け加えて考えてみてください。そうすると、演繹法と同様にストーリーができて、考えがまとまりやすくなります。
※範囲を意識:この問題の範囲は、結論にある「このプロジェクト」です。
■論理思考の利点
論理思考は理詰めで話をするので、説得や説明に向いています。特に、今回ご紹介した演繹法や帰納法が使えると、相手が論理的に話をしているかどうかも分かってきます。これは会話をする上で非常に有効な点だと筆者は考えています。演繹法や帰納法は普段でも使える考え方ですので、ぜひ使ってみてください!