乱数を用いたシミュレーション1　モンテカルロ法

高校情報科内講座2学期編

» 2021/07/12

まずは、削除した前回の「お休みのお知らせ」に「残念です。 次回期待して待っております。」と応援コメントをくださった匿名の方、ありがとうございます。

実はこの乱数を用いたシミュレーションの話が終わると2学期末テストに向けた内容になるので、試験問題を考えるのと内容考えるのと昼の仕事が7月からシフトになって土日出る日が出てきたのでいっぱいいっぱいになっちゃった結果が先週のお休みとなりました。
一般的には12月中旬に期末テストで、本ブログではそれを3か月前倒してるから9月中旬では？
https://el.jibun.atmarkit.co.jp/hfukkoshi/2021/03/post_13.html　でも8月と書いてるし、という方　ごめんなさい。
授業を実施する際はプログラミング問題の出題とか、ピクトグラム等々の問題解決作品を考えてみるなどの実習の時間で本来あとの8時間(週2時間×4週)を埋めるのですが、流石にエンジニアライフ上でその作成をお願いするのは無理があるとの結論になりました。

なので、1～2回は問題の紹介するにしても7月末くらいには試験にする、という方針にさせていただきます。
暫定7/29に問題公開、1学期末試験同様8月は受験待合期間、9月～12月に3学期編で計画再修正とさせていただきます。

---

で、今回の本筋。
前回シミュレーションにおいては「モデルが正しくないと意味なくね？」という話をしました。

で、多少なりともモデルをリアルに近づけるため、乱数を利用して解くという方法があります。
その方法として応用情報以下で出てくるのはモンテカルロ法と待ち行列理論になります。
待ち行列理論についてはガチで書き出すと大学の2単位講義丸ッと埋まるレベルになるので次回に回します。(それでも触りくらいのことしか書けなさそうだけど)

で、モンテカルロ法については今回やります。

モンテカルロ法とはシミュレーションする際、乱数を用いて大量に実行し、その結果をもとにシミュレートする方法である。
一例として、x,y∈R,0≦x≦1,0≦y≦1　(x,yはともに0～1の実数)で乱数によって決定するものとする。
で、原点を中心とする半径1の円があったとき、円内をtrue,円外をfalseとする

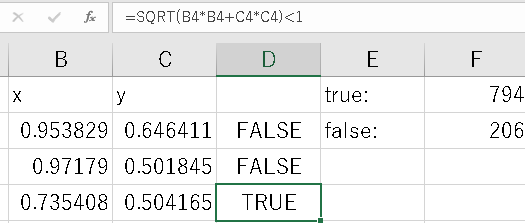
下の図でいうと赤いところがtrue、黄色いところがfalseになる計算だ。

で、この内部で1000この点を存在させ、true,falseを分類したのが上の表である。

実際の計算だと正方形全体は1辺1の正方形なので1。赤い部分はπ/4。近似して0.7854。
なので215個くらいはfalseになってもおかしくないね。

このように乱数を用いることで結果を近似することができるのである。
他に、洗牌を計算して天鳳天和の計算率を出したり(友人が作ってみたところ0.28 0.0030%だったそうだ⇒吹越の記憶ガバでした。友人に10年前のプログラム動かしてもらった結果)

https://twitter.com/Ratta86/status/1416631396580216832

遺伝的アルゴリズムでも個体の生成を完全ランダムのみにした場合はモンテカルロ法と呼んでよい状態になる。

こんなシミュレート方法もあるんだなーと思っていただけると嬉しい。
まぁ、基本情報の午前問レベルだが・・・。