オーダー (どのくらい計算に時間かかるん?)
今回の内容は完全に高校情報科の範囲ではなく、大学のコンピュータサイエンスのレベルです。
基本情報など、情報処理技術者試験系に出てくる内容なので、把握しておいてほしい内容になります。
前回の怪文書よりはましな内容かとw。
アルゴリズム
同じ結果を求めるのにも、「やり方」を変えるとかかる時間がちゃうねん、というのは割と知られた事実です。
情報処理の場合、そこで最も多用される例題は「ソート(並び替え)」アルゴリズムです。
なんでかというと「サーチ(探す)」ことをする場合、ソートされてないと「頭から全部見る」しか探す方法が無いからです。
例えばシャッフルされたトランプ1セット52枚(ジョーカーは抜いている)でハートのエースを探せ、と言われた場合、頭から1枚ずつめくるしかない。
でもこれが高々50枚くらいのトランプならまだ頭からめくっていってもそんなに時間がかからないと思う。
でも検索対象が順番がバラバラな単語カードだったら?その単語カードの枚数が辞書の単語数並みにあったら(数万枚)?
1枚1枚めくるのは馬鹿のやることだということは納得してもらえると思う。あるいは見落としても気づけないかもしれない。
なので、「探すにはある目的順で並んでるほうが効率がいい」ということには納得してもらえるだろう。
ちなみに紙の辞書を調べるとき、索引順に並んでいるわけだから「大体この辺にある」というページに当たりをつけて開くだろう。
コンピュータにはそれができないので、バイナリサーチ(二分探索)という方法がある。
トランプの例でバイナリサーチを考えてみる。
ここではトランプが強い順に並んでいるものとする。
諸説あるが、強いの定義は「マークが♠♥♦♣の順、マーク内ではA,K,Q,J,10,9,8,7,6,5,4,3,2の順」とする。
♠Aが最強で♣2が最弱である。
この状態でトランプが並んでおり、♥9を探すとする。
手順は「ちょうど真ん中になるカードで2つの山に分ける。奇数の場合は後半の山を1枚多くする。後半の山の1枚目のカードを確認する。探していたカードなら終了。探していたカードでないならカードがあるほうの山を選んでこの手順を繰り返す。」である。
52枚のカードのうち、1回目の操作で26枚づつの山に分ける。後半の山の1枚目を見る。♦Aだ。♥Aは前半26枚の中にある。
26枚のカードのうち、2回目の操作で13枚づつの山に分ける。後半の山の1枚目を見る。♥Aだ。♥9は後半13枚の中にある。
13枚のカードのうち、3回目の操作で6枚,7枚の山に分ける。後半の山の1枚目を見る。♥8だ。♥9は前半6枚の中にある。
6枚のカードのうち、4回目の操作で3枚づつの山に分ける。後半の山の1枚目を見る。♥Jだ。♥9は前半3枚の中にある。
3枚のカードのうち、5回目の操作で1枚,2枚に分ける。後半2枚の大きいほうを見る。♥10だ。♥9は前半2枚の中にある。
2枚のカードのうち、6回目の操作で1枚づつに分ける。後半のカードを見る。♥9だ。見つけた。探索終了。
という手順を踏む。トランプの場合、調査回数が最多で6回比較すればデータがあるかどうかを区別できる。
これは「頭から全部めくって探す」より効率的な方法だと納得できるだろうか?
ちなみに「頭から全部めくって探す」を情報工学的には「リニアサーチ」という。
Order記法(略してO記法)
上の話で「リニアサーチ」と「バイナリサーチ」で比較回数がバイナリサーチのほうが少ない、という話をした。
「でもそれはトランプの50枚程度の話だろう?」と思われるかもしれない。
なので数学的に拡張して、「N個のデータの中から1つのデータを探す(あるいは見つからないことを証明する)」ことを考えてみる。
このとき、リニアサーチはN回のチェックを必要とするのでNに正比例する。
バイナリサーチはNに対して半分・半分と割っていくのでlog_2(N) ※底が2の対数 となる。
この2つの関数をグラフ化するとこのような感じになる。
※グラフではNではなくxを用いているが、関係性は同じである。グラフ作成は「https://www.geogebra.org/graphing?lang=ja」を利用した。
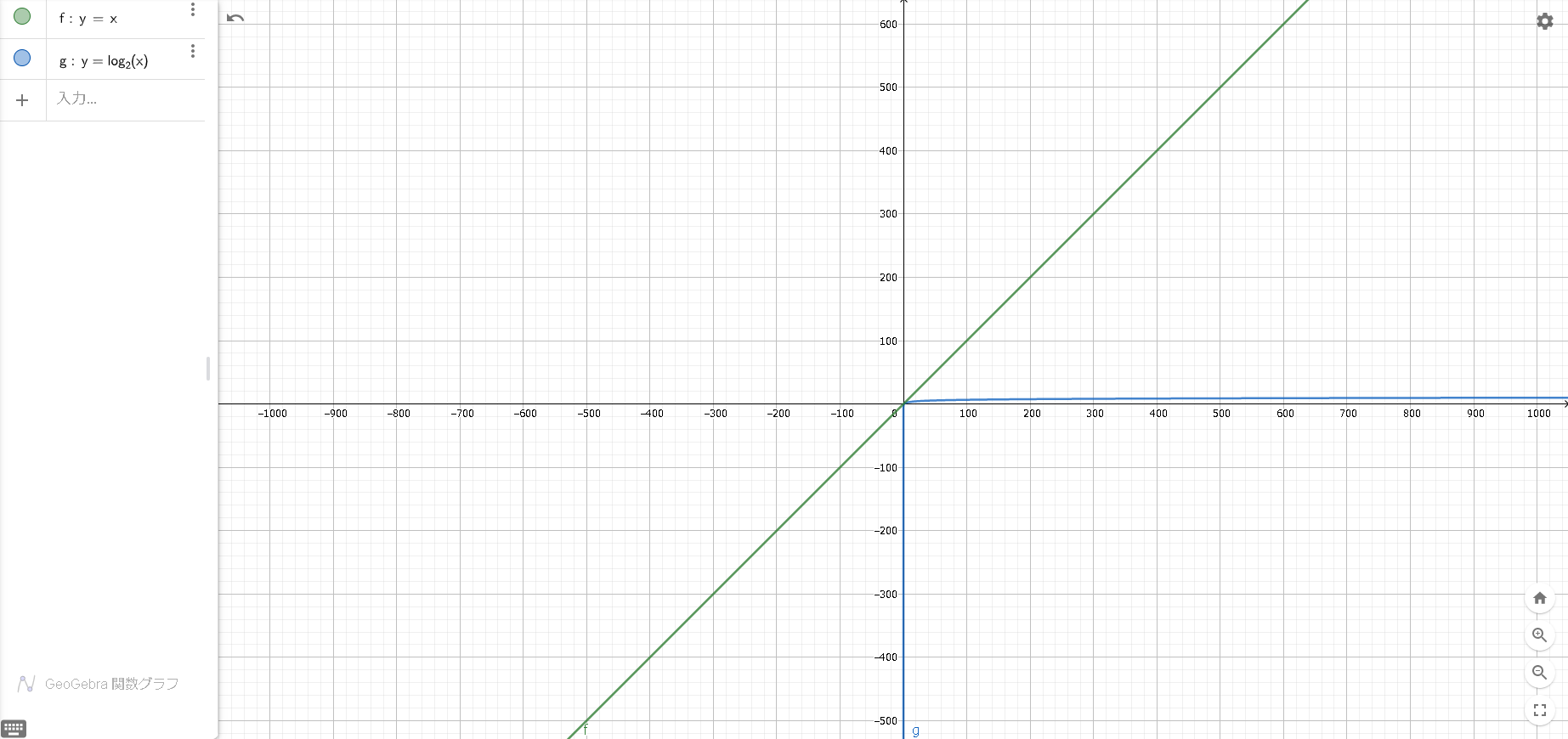
圧倒的にバイナリサーチのほうが「伸びが悪い」ことに納得いただけるだろうか?
つまり「データ数が多くなってもあんまり時間が変わらない」という特徴があることがわかる。
そこで、情報数学においてはこの計算回数の効率が良いか悪いかでアルゴリズムを分類しよう、という時期があったのだ。
(今ではCPUの計算速度が上昇したので、多少遅くても可読性の良いコードのほうが良いとか、セキュリティ的にしっかりしているほうが良いパターンもあるが、原則として計算回数が少ない=効率の良い方法である。)
その際の比較として出てきた書き方がO記法(おーきほう)である。
O記法を用いて書くと、リニアサーチはO(N)、バイナリサーチはO(LogN)と書かれる。
書き方としては「N個のデータに対して、Nが指数を持つ場合は指数が最大の項だけ(しかも係数は不要)を書く」である。
あるアルゴリズムの計算回数が詳細に「5N^2 +6N+2」回と判明したとする。
これをO記法で表現する場合はO(N^2)となる。係数5や他の項は無視する。
なんでかというと、「Nが1万とか10万とか100万とかになった時に差があんまりないわー」という理由である。
もちろん係数が巨大数並みに大きいと影響するのだが、O記法のルールとしてそこには触れないことになっている。

ということでアルゴリズムにおいては良し悪しを比較するのにO記法というものを用いる。
オマケだが、元データの並びにおいてもアルゴリズムは回数の影響を受けるのだが、最悪パターンを想定する場合はΩ(オメガ)で書くし、最高効率を考えるときはo(小文字のオー)で書く。
O(大文字のオー)は「平均的なパターンの時」という考え方で実施する。
サーチアルゴリズムの計算量
サーチアルゴリズムはぶっちゃけ先のバイナリサーチが非常に効率がよくてよく使われる。
リニアサーチは遅い部類(理由は上を見ればわかるでしょう?)。でも実はサーチアルゴリズムには最強のO(1) (※データ量にかかわらず同じ時間で検索・有無を返す) という滅茶苦茶なアルゴリズムもある。
それをハッシュマップというが、これを理解するにはハッシュ関数とは何か、という話が理解できてないといけなくて超長くなるので各自で調査してほしい。
「O(1) 計算量」とかでググるといい。
ソートアルゴリズムの計算量
サーチの前準備としてソートアルゴリズムの話をしたが、こちらはめっちゃ種類が多い。
そのうえで計算量の比較とすると「計算量の初歩」として動画を公開している人が滅茶苦茶たくさんいるので参照してほしい。
なお基本情報を覚えるうえではクイックソートとバブルソートを覚えておけば概ね困らない。
それ以外のソートについては興味があったら調べてみてほしいし、トランプとかで実践してみてほしい。
以下は吹越が見つけたソートに関する動画である。
https://www.nicovideo.jp/watch/sm37443044
https://www.youtube.com/watch?v=BeoCbJPuvSE
P≠NP問題
完全なる蛇足であり、情報処理技術者試験にも出てこないガッチガチの情報数学最高難度の問題。
この計算量に関する問題が関わってるので一応紹介。
問題を解こうとすると「N!パターンやe^Nパターンのデータから最高効率の1つを選べ」なんて問題がよく出てくる。
巡回セールスマン問題やナップザック問題というやつで、この手の「指数的時間」の問題は完全な解を出すのに解答の全パターンを出す必要があるので最適解を保証すると滅茶苦茶時間がかかる。
でもこの手の問題の中には「検算はクッソ早い」というパターンのものがある。
さて、「N!パターンから最適解を出せ」という問題のグループ全体と「その中でも検算はクッソ早い」グループは完全に一致するのか?(つまり知られてないだけで超早く解く方法があるのか?)それとも「そんなもんはない」のか?
という問題である。なんでこれが超注目されるかというと、現代の暗号理論がこの「最適解を出すのは超 時間がかかる」けど「検算はクッソ早い」という性質を利用しているためだ。世界初の公開鍵暗号であるRSA暗号なんかはそれに該当する。というか公開鍵暗号は確か、大体該当するはず。
量子コンピュータがもてはやされる理由の一つにこの手の問題を高速に解くアルゴリズムが示されているからである。(ショアのアルゴリズム)
ざっくり資料にするならこの動画を見るとよろし。さっきのソートの人と同じ人だが。
むしろ吹越のより分かりやすいか・・・