両対数グラフを使えば、微分は簡単
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
＊ 両対数グラフを使えば、微分は簡単 ＊ ２０２５年 ４月２２日 Ricardo （リカルド）
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
- 「微分」とは関数のグラフを描いて、接線の傾きを調べる事です。
- 一次関数の微分
右の一次関数では、Ａが傾きになります。
- 関数の加算
下図左の切片成分は微分に影響しないので取り払い、右図の③④とします。③と④を加算すると、傾きは(A+C) となります。
- 軸の密度
右図は、４５度の傾きです。ですから、見掛けの傾きは１です。
しかし縦軸と横軸の密度が違います。
縦軸の密度
真の傾き ＝ 見掛けの傾き ＊ ―――――
横軸の密度
２
真の傾き ＝ １ ＊ ― ＝ ２
１
- 対数目盛り
等比目盛りです。同じ比率なら、同じ長さになります。
１と２、２と４の長さは同じになります。
右に行くと、密度が高くなります。密度は、その座標の値に比例します。
- y = ｘ^2 の微分
見掛けの傾きは、平等目盛りで見た傾きです。
ｘ^2
真の傾き ＝ 見掛けの傾き ＊ ―――
ｘ
＝ ２ ＊ ｘ
＝ ２ ｘ
- y = x^2 * 10 の微分
見掛けの傾きは、平等目盛りで見た傾きです。
x^2 ＊ １０
真の傾き ＝ 見掛けの傾き ＊ ――――――
ｘ
＝ ２ ＊ ｘ ＊ １０
＝ ２０ｘ
- y = a * (x^n) の微分
見掛けの傾きは、平等目盛りで見た傾きです。
a * x^n
真の傾き ＝ 見掛けの傾き ＊ ―――
Ｘ
＝ ｎ ＊ a * x^(n-1)
- 対数目盛りで乗除算
対数目盛を使うと、乗除算が加減算になります。
- F(x)G(x) の微分
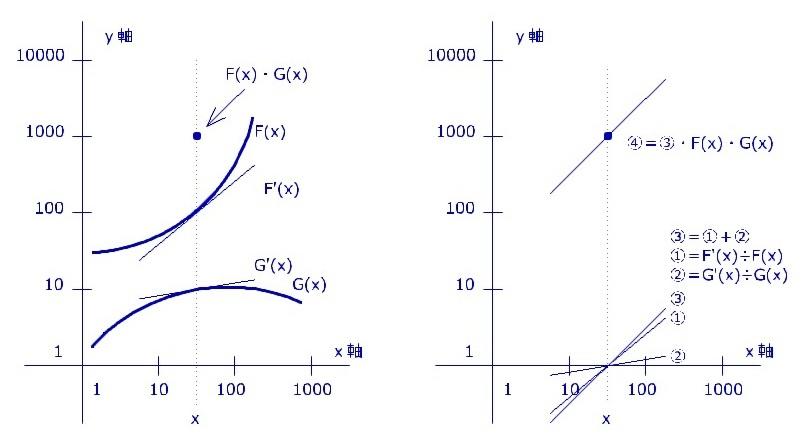
F(x)G(x)をｘの所で微分してみましょう。
右図左側のｘの所で接線を引きます。
右側で接線を y = 1 の所に持って行きます。
①と②を足すと③になります。③を④に持って行くと、最終的な答えになります。
- F(x)/G(x) の微分
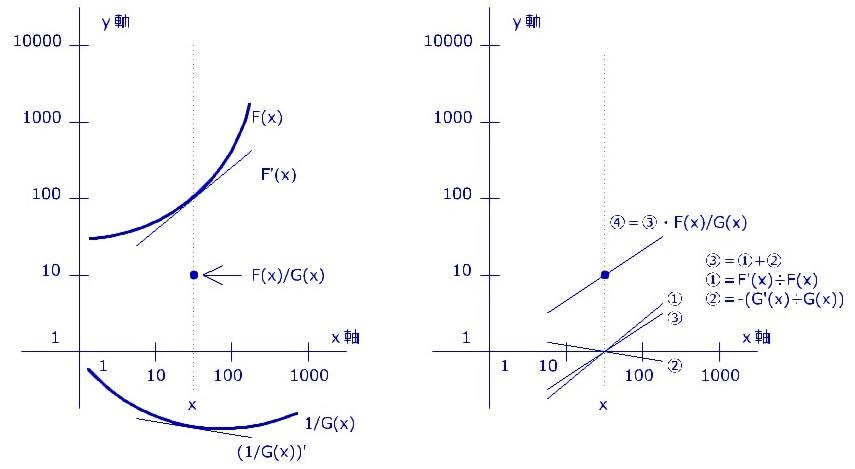
G'(x)とG(x)を y = 1 の軸を中心に反転させます。
①と②を足すと③になります。③を④に持って行くと、最終的な答えになります。
- 複雑な乗除算の微分
－－以上ーー